| 1. Princip Anaxiomatizace |
|---|
| 2. 3 zakřivené prostory . |
| 3.Extenze časoProstoru |
| 4 . Hyper-Rotátor HyR . |
| 5.Ovlivnění přitažlivosti |
| 6 . Formule Extenze . |
| 7 . Oslabení tíže . . . |
1. PRINCIP ANAXIOMATIZACE
Od vzniku Einsteinovy teorie Relativity uplynulo již více než století, takže je nejvyšší čas udělat v ní další vývojový krok : ještě více ji zobecnit a "hyperrelativizovat". Kvůli širšímu rozhledu je třeba se zbavit všech omezujících faktorů, apriorních axiomů : provést neklasickou Anaxiomatizaci .
Jejím učebnicovým příkladem je vytvoření Neeuklidovských geometrií na konci 19.století : Riemann, Lobačevskij a další odmítli 5. Euklidův axiom o rovnoběžkách jakožto omezení vědeckého poznání - a to jim umožnilo vybudovat nové, neklasické geometrie.
V následujícím století matematik Gödel pak ještě dokázal, že každý axiomatizovaný výrokový systém je nutně neúplný a nerozhodnutelný, t.j. chybí v něm některé pravdivé výroky (věty, teze) a naopak obsahuje výroky, o jejichž pravdivosti nemůže rozhodnout. Tím exaktně potvrdil intuitivní názor o omezujícím vlivu axiomů v matematice - a postulátů i dogmat všude v lidském poznání .
Na počátku 20.století Einstein odmítl Newtonovské axiomy o absolutnosti prostoru a času (klasickým fyzikům zdánlivě naprosto přirozené a nezpochybnitelně pravdivé), čímž dospěl k Teorii Relativity (Speciální). Později odmítl ještě i předpoklad o inerciálnosti vztažných systémů, takže mohl vypracovat Obecnou teorii relativity - což je další podstatný pokrok poznání světa .
Naším úkolem bude v tomto směru dále pokračovati, další Anaxiomatizací ještě více Relativitu zobecnit.
Omezující postulát limitní rychlosti světla c = 299 792 456 m/s totiž budí podezření, že Einsteinova teorie není ještě úplně nejobecnější (tento axiom vyvolává Gödelovskou neúplnost). A to vede k nekonformní otázce : Lze dosáhnouti dalšího pokroku fyziky odmítnutím axiomu Konstantní světelné rychlosti - přece její absolutnost narušuje konzistenci a obecnost Relativity (jejímž je protimluvem) ?
Proto v zájmu dalšího pokroku vědy je třeba tento standardní předpoklad zrušiti jakožto přežitek z minulého století. V nové anaxiomatizované Teorii Hyper-Relativity (viz 9. kapitola) už neplatí žádné zastaralé postuláty, omezující náš světonáhled (méně axiomů znamená obecnější a úplnější teorie). A obsahuje v sobě starou Einsteinovu obecnou Relativitu jako zvláštní případ - analogicky jako Einsteinova teorie v sobě zahrnula předchozí Newtonovskou fyziku...
Pro náš účel je zvláště důležitá Anaxiomatizace v geometrii . Už v 19.století s ní začali Riemann, Lobačevskij, Bolyai a další . Ukázalo se, že Eukleidovská geometrie, do té doby považovaná za jediný možný popis světa, nemá všeobecnou platnost. Potíže s 5. Eukleidovým axiomem ukázaly její neúplnost ; prostor nemusí býti pouze klasicky rovný (plochý) - nýbrž také zakřivený : Riemannovsky kladně nebo Lobačevsky záporně.
2. 3 ZAKŘIVENÉ PROSTORY
Trojrozměrný křivý prostor však nelze nakreslit ani si jen představit, poněvadž naše myšlení a představivost se vyvinuly v nezakřiveném plochém světě pod vládou Eukleidovy geometrie : Zde jsou přímky rovné, úhly v trojúhelnících mají součet 180° a obvod o každého kruhu je 2π násobkem jeho poloměru r . Daným bodem A lze vést právě jednu rovnoběžku q k zadané přímce p (toť 5. Eukleidův postulát).
Obrázek 1.: Eukleidovská geometrie v rovině (s nulovou křivostí) :
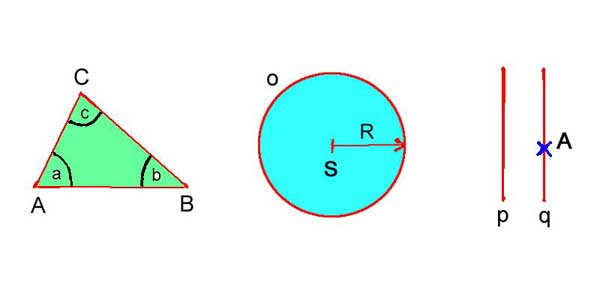
Takové zakřivení má povrch koule, a proto se této geometrii taky říká sférická .
Obrázek 2.: Riemannovská geometrie na kouli (s kladnou křivostí) :
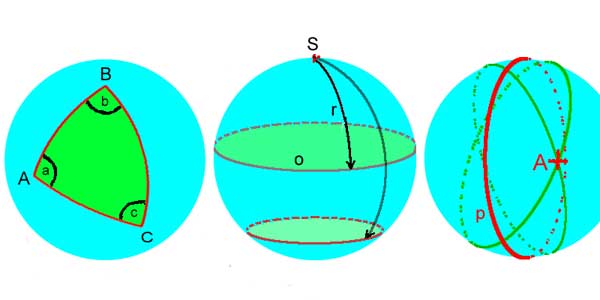
Tyto podivuhodné vlastnosti má povrch hyperboloidu - proto se Lobačevská geometrie nazývá též hyperbolická .
Obrázek 3.: Lobačevská geometrie na hyperboloidu (záporné zakřivení) :
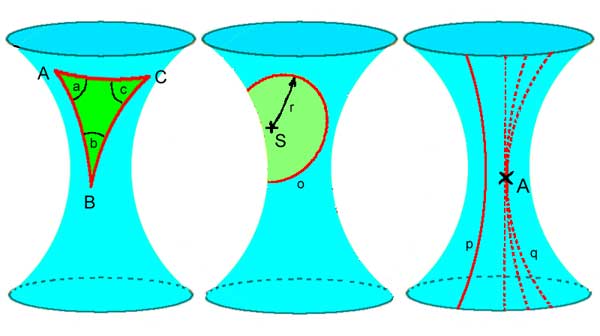
Skutečný prostor je trojrozměrný a Vesmír, kde žijeme, má navíc ještě i čtvrtou dimenzi : čas . Speciální teorie Relativity objevila, že náš svět je ve čtyřrozměrném časoprostoru a Obecná teorie Relativity pak dospěla k poznání, že může být i zakřivený.
Čtyřrozměrnou křivost lze pochopit z analogie s dvourozměrnou ; a taktéž může být kladná, nulová (bez zakřivení) či záporná.
V případě absence hmoty a nepřítomnosti gravitačního pole (v čistém vakuu) je časoprostor nezakřivený (plochý) a platí v něm normální Eukleidova geometrie. (Ta je skoro přesná i ve slabých gravitačních polích, jaká jsou běžná všude kolem nás.)
3. EXTENZE HYPERBOLICKÉHO ČASOPROSTORU
Podle Obecné teorie Relativity hmotná tělesa kolem sebe zakřivují časoprostor kladně, takže v něm už neplatí geometrie Eukleidova, nýbrž Riemannova. A naopak kladné zakřivení časoprostoru se fyzikálně projevuje jakožto gravitační pole . Pak nabývá platnosti sférická geometrie Riemannova a metrika dostává nezvyklé vlastnosti, jak znázorněno na Obrázku 2. Dochází ke kontrakci (smrštění) prostoru a navíc je ovlivněn i čtvrtý rozměr : čas se zpomaluje (dilatuje).
[V krajním případě supersilná gravitace dokáže zakřivit časoprostor tak, až se úplně uzavře do t.zv. "Černé Díry" (Kolapsaru), kde se čas zastaví a prostor zauzlí v singularitu.]
V zakřiveném prostoru se světelné paprsky nepohybují po přímkách, ale jsou nuceny taktéž se zakřivit. Gravitační pole veliké hmoty (například Slunce) způsobuje ohyb světla . Pozorování tohoto jevu při zatmění Slunce roku 1919 bylo jedním z důkazů správnosti Obecné teorie Relativity.
Ještě větší hmota (třeba galaxie) dokáže paprsky zkřivit podobně jako spojná čočka a soustředit je do ohniska. To bylo již také několikrát vyfotografováno v nedávné době při zkoumání Kvazarů.
Tenzorové vyjádření gravitačního pole v Einsteinových rovnicích pak znamená, že přitažlivá gravitace vlastně představuje jakési kladné napětí, smršťující tenzi časoprostoru, která koncentruje, fokusuje světočáry .
A vzhledem k symetrii přírody (všechno má i svůj opak) lze očekávat i existenci napětí opačného, záporného : expandující tenzi, extenzi časoprostoru, která dissipuje, rozptyluje světočáry. Odpovídá opačnému (zápornému) hyperbolickému zakřivení časoprostoru a vyvolává i opačné fyzikální efekty : dilataci (rozepnutí) prostoru a kontrakci (urychlení) času.
Taková opačná křivost časoprostoru s hyperbolickou Lobačevskou geometrií se patrně bude projevovati také opačně než gravitace : odpudivě . Expandující prostor totiž zvětšuje mezilehlé vzdálenosti všech objektů, které se v něm i kol něj nacházejí. Ty se tak od sebe navzájem odtahují, jakoby mezi nimi působila odpuzující síla, opačná přitažlivosti.
Proto bude vhodnější název Extenze Hyperbolického ProstoroČasu (zkr. EhyP).
Odkud by však ta neklasická EhyP mohla pocházet ? Přece hmota (i antihmota) je zdrojem gravitace ekvivalentní kladné křivosti časoprostoru a v prázdnotě (vakuu) je zakřivení nulové.
Takže nezbude než konstatovat, že samotný časoprostor se zápornou křivostí, charakterizovanou Lobačevskou hyperbolickou geometrií - tedy jakési "negativní" (hyperbolické) vakuum - je výhradním zdrojem EhyP.
Není to však pouhá nereálná hypotéza ?
Einstein zprvu ve svých rovnicích počítal s t.zv. Kosmologickou konstantou Λ (Lambda), která představovala odpudivé vlastnosti prázdného časoprostoru, působící proti gravitaci (aby se Vesmír nezhroutil). Ta by mohla popisovat záporné zakřivení časoprostoru, odpovídající té hyperbolické Lobačevské geometrii . (Později však od Kosmologické konstanty ustoupil.)
Z principu Anaxiomatizace nicméně vyplývá, že apriori nelze vyloučit žádnou možnost. Přece žádné dogma netvrdí, že zakřivení časoprostoru může být výhradně a pouze kladné nebo nulové - a nikoli záporné . To, že jsme se doposud setkávali jen s geometrií Eukleidovou nebo Riemannovou, absolutně nevylučuje ještě Lobačevského hyperbolickou geometrii.
4. RELATIVISTICKÝ HYPER-ROTÁTOR HYR
Reálnou možnost negativně zakřiveného časoprostoru znázorňuje následujícím model :
Obrázek 4.: Působení Hyper-Rotace :

Představme si kotouč z nedeformovatelného materiálu zanedbatelné hmotnosti, který roztočíme tak, aby se jeho obvod pohyboval téměř rychlostí světla. Pak se tam budou projevovat efekty Speciální teorie relativity : kontrakce (zkrácení) délek a dilatace (zpomalení) času . Hypotetický pozorovatel na kotouči pak zjistí, že tam vlivem relativisticky rychlé rotace už neplatí normální Eukleidovská geometrie :
Když vezme tuhé decimetrové měřítko a přiloží je na obvod rotujícího kotouče (levá strana obrázku), tak se relativisticky zkrátí (b), poněvadž se pohybuje téměř rychlostí světla. Aby pozorovatel změřil obvod rotujícího kotouče, musí takto zkrácené měřidlo přiložit vícekrát, než kdyby kotouč stál (v tom případě by se měřítko nezkrátilo) a proto naměří více decimetrů.
Naproti tomu, když měří poloměr kotouče, měřidlo se mu nezkrátí (a), protože je kolmo k rychlosti pohybu. Poloměr r tedy naměří stejný jako u stojícího kotouče (předpokládame-li jeho dostatečnou tuhost aby odolal odstředivé síle ; nebo ji odkorigujeme výpočtem z koeficientu protažení materiálu). Poněvadž obvod kotouče o pozorovatel naměřil delší, tak platí neeukleidovské : o > 2πr .
Podobně když pozorovatel sleduje dráhy světelných paprsků blízko obvodu rotujícího kotouče (na pravém obrázku), tak zjistí, že se nepohybují po přímkách, nýbrž jsou konkávně zakřiveny vlivem relativistických efektů : Blíže u obvodu jsou vzdálenosti mezi vlnoplochami světla kontrahovány , takže vlna se ohýbá k obvodu rotátoru. A také se směrem k obvodu zpomaluje čas, takže vlnoplochy tam mají menší rychlost a proto se elektromagnetické vlny tím směrem ohýbají . [Lépe je to vysvětleno u následujících Obrázků 5. a 6. v příští kapitole.]
I strany trojúhelníků (ABS) jsou tam konkávně vyduté, takže součet vnitřních úhlů je menší než 180° . Ani pro rovnoběžky (p, q) už neplatí 5. Eukleidův axiom - vinou jejich zakřivení, jak ukazuje pravá strana obrázku.
Nejsou však tyto jevy pouhým zdáním pozorovatele na rotátoru ?
Tyto efekty jsou objektivně změřitelné fyzikálními přístroji a stejně skutečné jako okolní realita. Podle principu relativity jsou všechny fyzikální soustavy i hlediska (na Hyper-Rotátoru i mimo něj) stejně relevantní a nikdo nemá právo považovat výhradně svoje pozorování za správnou skutečnost a druhá jenom za pouhé iluze.
Ostatně Hyper-Rotátor by bylo možno uzavřít ze všech stran (jako některé typy kolotočů), takže by pozorovatel ani nemusel vědět, že se točí - a přece by popisované jevy zaregistroval.
Svoji rotaci by přece pozorovatel zjistil podle odstředivé síly ?
Tu by bylo možné libovolně zmenšit při dostatečně malé frekvenci otáčení . Představme si například fantastický rotátor o poloměru milion světelných let, který by se otočil dokola jedenkrát za 6,283 milionu let. Jeho úhlová rychlost rotace by byla nepatrná a takřka nezjistitelná (biliontina rad/sec) a odstředivá síla zanedbatelná (miliardkrát menší než pozemská přitažlivost).
Však jeho obvod by se pohyboval téměř rychlostí světla, takže by se tam v plné míře projevovaly ty výše popsané relativistické efekty ! Tamní pozorovatel by si vůbec nemusel povšimnout, že rotuje (tak nesmírně pomalu), ani tu nepatrnou odstředivou sílu by nezaregistroval. Zjistil by však, že ten zdánlivě nehybný kotouč je zdrojem nějakého podivného působení, které hyperbolicky zakřivuje prostor u okraje (pozměňuje geometrii na Lobačevskou) a relativně zrychluje vnější čas : tedy vyvolává zápornou křivost časoprostoru a jeho Hyperbolickou Extenzi.
5. OVLIVNĚNÍ PŘITAŽLIVOSTI
Obrázek 5.: Radiální zakřivení - divergentní (vlevo) a konvergentní (vpravo) :

Levý obrázek ukazuje průchod světelných paprsků (znázorněných červenými šipkami) relativisticky rotujícím HyRem (kdyby například byl průhledný - kdyby byl neprůhledný, mohly by se použíti třeba Rentgenovy paprsky). Jeho obvod dosahuje téměř rychlosti světla, takže tam dochází k efektům Speciální teorie Relativity :
- Dilataci času , t.j. zpomalování veškerých dějů (včetně pohybu světla). Světelné vlnoplochy (modré čárky kolmé k paprskům) se na straně bližší k okraji rotátoru pohybují pomaleji než na vzdálenější straně, takže vyvolávají zakřivování světelných paprsků směrem k okraji.
- A kontrakci prostoru : vlnoplochy se směrem k obvodu Hyper-Rotátoru zhušťují , jelikož vzdálenosti mezi nimi se tam smršťují. Takže se světelná vlna tím směrem ohýbá .
Hyperrotace vyvolává opačný efekt než je známé parabolické zakřivení světla způsobené silným gravitačním polem těžkého tělesa T na pravém obrázku.
Zde pak nastupuje Obecná teorie Relativity : v blízkosti těžké hmoty se zpomaluje (dilatuje) čas a smršťuje (kontrahuje) prostor . Proto se blíže k T vlnoplochy pohybují pomaleji a vzdálenosti mezi nimi kontrahují (jak ukazují modré čárky). Světelné paprsky (červené šipky) se tak zakřivují směrem k centru přitažlivosti.
(Tento projev konvergující deformace časoprostoru (ohyb světla) působením gravitace byl odvozen Einsteinem a pozorován Eddingtonem již téměř před sto lety ; je jedním z klasických důkazů Obecné teorie Relativity.)
Obrázek 6.: Axiální zakřivení - divergentní (vlevo) a konvergentní (vpravo) :

Na tomto obrázku dále vidíme, že k hyperbolickému zakřivování dochází i když paprsky Hyper-Rotátorem procházejí ve směru jeho rotační osy (musí ovšem být HyR dosti tlustý, válcový). U pláště válce rotujícího relativistickou rychlostí dochází ke zpomalování času a smršťování prostoru, čímž se také vlnoplochy tam zpomalují a zhušťují, což vede k ohýbání paprsků směrem ven . Ohnutí je v tomto případě závislé i na tloušťce HyRu, protože čím delší dráhu urazí světlo (či jiné částice) v oblasti časoprostoru deformované hyperrotací, tím více se také odchýlí od původního přímého směru.
(Také zde vidno, že se nejedná o žádnou odstředivou sílu, poněvadž ta na tloušťce rotátoru samozřejmě nezávisí - pouze na jeho poloměru - a na světelné vlnoplochy nepůsobí vůbec.)
Jistě by nedalo moc práce ukázat, že k popsaným efektům dochází i při jiných směrech dopadajícího světla (při vhodném tvaru rotátoru) a také, když paprsky jdou opačně, t.j. zespodu . Tedy to divergentní působení HyRu nezávisí na směru - takže je analogické působení gravitace, která je také všesměrová (arci opačná, konvergující).
Následující Obrázek 7. ukazuje, kterak Hyper-Rotátor (na pravé straně) oslabuje zemskou přitažlivost. Její gravitační siločáry znázorňují červené linie. Na levě straně obrázku (bez HyRu) všechny "zasahují" přitahované těleso T . Na pravé straně HyR zakřivuje všechny světočáry (tedy i gravitační siločáry) hyperbolicky a dissipuje je, takže se "zředí" a některé odchýlí mimo T . Těleso pak zasahuje méně gravitačních siločar, tudíž i síla přitažlivosti se zmenší :
Obrázek 7.: Dissipace gravitace :
.

6. FORMULE EXTENZE
Při velmi vysoké rychlosti Hyper-Rotátoru se na jeho okraji kromě klasické odstředivé síly objevuje ještě další vliv, který má čistě relativistický původ :
Hmotnost předmětů na obvodu se totiž vlivem jejich skorosvětelné rychlosti relativisticky zvětší, takže jejich setrvačné působení o hodně převýší normální odstředivou sílu. Také prostorové a časové relace se tou hyperrotací změní, což nezůstane bez následků pro tamní síly a zrychlení :
- Z klasické mechaniky známe vzorec pro standartní odstředivé zrychlení N (m/s2), platný pro obvyklou rotaci . Zde je r (m) poloměr rotátoru a T (s) je oběžná doba rotace.
- Při extrémní obvodové rychlosti v (m/s) hyperrotace bude odstředivá síla v důsledku relativistického nárůstu hmotnosti větší a dojde i ke kontrakci délek a dilataci času - takže se odstředivé zrychlení zvětší na relativistické R (m/s2) ; c (m/s) je známá rychlost světla.
- Vzorec pro klasickou obvodovou rychlost v (m/s) rotátoru.
- Po odečtení normálního nerelativistického odstředivého zrychlení N dostaneme čistý relativistický příspěvek hyperrotace A (m/s2).
- Po zjednodušení tohoto výrazu a dosazení za v z (III.) nakonec získáme výsledné A :
 |
A (m/s2) je skalární intenzita Extenze Hyperbolického ProstoroČasu, vytvářené Hyper-Rotátorem. Má stejný rozměr zrychlení jako intenzita gravitačního pole, vytvářeného hmotnými tělesy (jsouc jeho negací).
Ve vzorci (V.) ta první konstanta (2π)4 upozorňuje na jeho geometrickou povahu, poněvadž Ludolfovo číslo π je nezbytnou součástí všech geometrických vztahů.
Kvadrát rychlosti světla c-2 pak vyjadřuje relativistickou podstatu A , poněvadž vystupuje ve formulích Teorie Relativity. Způsobuje také zanedbatelnou nepatrnost EhyP při normálních okolnostech, protože má hodnotu pouhých sto triliontin (10-16).
Faktor T4 ve jmenovateli představuje velmi silnou závislost na oběžné době (periodě) rotátoru : teprve když je velice nízká (t.j. velmi vysoká frekvence a rychlost otáčení), začne se projevovat Extenze Hyperbolického ProstoroČasu. Při obvyklých rychlostech otáčení je EhyP nepozorovatelná.
Činitel r3 ukazuje, že velikost Hyperbolické Extenze je dána velikostí prostoru Hyper-Rotátoru - neboť (4/3)πr3 = V je objem koule, opsané HyRu - což je dalším svědectvím, že zdrojem EhyP je právě prostor Hyper-Rotátoru.
 |
Ve výsledném vzorci (V.) pak ten poslední relativistický činitel (B1) poukazuje na fakt, že A podstatně narůstá nejen při extrémní velikosti rotátoru r nebo malosti jeho rotační periody T.
Nýbrž také, když platí : (B2) ; neboli jeho obvod dosahuje rychlosti světla, t. j. platí (B3).
To je samozřejmé ; tehdy relativistická hmotnost okraje nekonečněkrát vzroste, čas na obvodu se zpomalí k nule a délka obvodu naroste k nekonečnu - dojde k extrémní hyperbolické deformaci Lobačevského časoprostoru.
(Analogicky v Obecné teorii Relativity dosahuje gravitační síla F extrémní velikosti nejenom pro nekonečně velkou přitažlivou hmotu M nebo nulovou vzdálenost d, jak plyne z klasického Newtonova zákona : (B4). Ale i tehdy, když platí (B5), t. j. na relativistické Schwartzschildově sféře, kde úniková rychlost hmotných objektů dosáhne rychlosti světla a platí : (B6).
I z tohoto vidíme symetrii mezi gravitací a Extenzí Hyperbolického ProstoroČasu.)
Ze vzorce /V./ pak snadno vypočítáme například, že rotace kotouče o poloměru r = 38 cm rychlostí 10 000 otáček za sekundu vytváří EhyP s intenzitou A = 9,4 m/s2 (přibližně), což je téměř rovno zemskému gravitačnímu zrychlení.
Takový Hyper-Rotátor by tedy mohl značně oslabit zemskou přitažlivost ; a při větším poloměru nebo rychlosti otáčení ji snad úplně zrušit.
A pole vytvářené Hyper-Rotátorem je značně nehomogenní : nejsilnější EhyP je kolem okraje, zatímco směrem do středu velice slábne (jak vidno ze vzorce /V./) . Aby se to vyrovnalo, bude třeba do středu Hyper-Rotátoru dáti ještě další menší, který tam bude přídavným zdrojem Hyperbolické Extenze ; do jeho středu opět další atd . Lepší generátory EhyP tedy budou tvořeny soustavou prstencových resp. toroidálních rotátorů, koncentricky vložených jeden do druhého.
7. OSLABENÍ TÍŽE ...
Však jako je princip ovlivnění přitažlivosti překvapivě jednoduchý, tak nesmírně složitá bude jeho technická realizace . Ta extrémní rychlost hyperrotace je na hranici současných možností.
Jak třeba zabránit roztržení rotoru obrovskou odstředivou silou a udělat ložiska fungující při tak vysokých rychlostech ?
Nejlepší ložiska však jsou žádná ložiska.
V moderních ultracentrifugách není rotor upevněn v nějakých pevných ložiskách, ale vznáší se (levituje) buďto v proudu vzduchu, nebo v magnetickém poli . Prvního způsobu ovšem na Hyper-Rotátor nelze použít, poněvadž ten musí rotovat ve vakuu : vzduch by jej brzdil a svým třením při ohromné rychlosti rozžhavoval. Využije se magnetické levitace, která je už dobře technicky zvládnuta :
Rotátor bude zhotoven z ferromagnetického materiálu (třeba ze superpevné slitiny Železa, Niklu a Kobaltu) a umístěn do evakuovaného pouzdra (z nemagnetického materiálu) ; které též zabrání rozletění úlomků při jeho možném roztržení . Kolem se rozmístí axiální soustava elektromagnetů, jejichž síla bude rotor udržovat právě uprostřed pouzdra, aby se ničeho nedotýkal. Automatické zařízení bude měřit vzdálenost od stěn (opticky nebo kapacitně) a podle toho regulovat sílu elektromagnetů k dosažení optima.
Aby se rotátor neroztrhl, budou proti jeho obrovské odstředivé síle působiti další magnetická pole. V cyklotronech se částice pohybují mnohem většími rychlostmi a jejich odstředivou sílu kompenzuje magnetické pole, které zakřivuje jejich dráhu do kruhu. Takže okolo HyRu budou ještě další elektromagnety, vytvářející radiální dostředivé pole, vyrovnávající odstředivou sílu (jeho intenzita samozřejmě se zreguluje podle rychlosti otáčení).
A konečně bude nezbytný ještě třetí systém cívek : motordynamický - jako v elektromotoru nebo v dynamu - pro urychlování nebo zpomalování rotace. Tím se bude ovládat intenzita EhyP : při zdvojnásobení rychlosti otáčení se zvětší 16x (poněvadž je úměrná 4. mocnině, jak udává formule /V./ v minulé kapitole) ; zbrzděním se analogicky silně zmenší.
Při brzdění se bude používat rekuperace (jako u elektrických dopravních prostředků) : cívky budou fungovat jako dynamo přeměňující pohybovou energii na elektrickou. Ta se uloží do akumulátoru a později zase použije při urychlování, kdy systém bude fungovat jako pohonný elektromotor. Veliké Hyper-Rotátory mohou mít díky své obrovské rychlosti zásobu kinetické energie asi jako rozjetý vlak, takže z ekonomických důvodů bude její rekuperace nezbytná.
HyR samozřejmě musí být umístěn ve vakuu , aby se třením o vzduch nepřehříval a nezpomaloval (uvnitř nějakého pevného pouzdra, které by též zabraňovalo rozletění úlomků při jeho případném roztržení). A pak se může točit setrvačností prakticky věčně podle Zákona zachování Momentu hybnosti. (Umožní to magnetická ložiska a závěsy, bez tření a bez opotřebení.)
Z principu činnosti HyRu vyplývá, že hlavním zdrojem Extenze Hyperbolického ProstoroČasu je jeho okraj, obvod , poněvadž pouze ten se pohybuje rychlostí blízkou světelné. Uprostřed jsou rychlosti podstatně nižší, takže tam k relativistickým efektům nedochází. O tom svědčí i vzorec /V./ v minulé kapitole, ve kterém faktor r3 ukazuje velmi silnou závislost na poloměru otáčení.
Vnitřní oblast Hyper-Rotátoru tedy k vytváření EhyP téměř nepřispívá, takže ji můžeme vypustit : stačí, když rotátor bude tvořen pouhým prstencem, uprostřed prázdným. Ochranné evakuované pouzdro pak bude míti tvar plochého toroidu . Prstencový HyR je také lehčí a v uprázdněném prostoru uvnitř mohou býti umístěna ovládací zařízení.
Helium je velmi lehké, takže odstředivá síla i pří ohromné hyperrychlosti nezpůsobí problémy ; ani roztrhnout se kapalný rotátor ovšem nemůže. Odpadnou tedy elektromagnetické systémy kompenzující odstředivou sílu a nahrazující ložiska (levitační). Taky energie potřebná na jeho urychlování bude mnohem menší, než u těžkých kovových kotoučů. Když bude He ionizováno, t.j. zbaveno jednoho elektronu, čímž se stane elektricky (kladně) nabitým, dá se ovládat elektrickými silami. A pak je můžeme zrychlovat (nebo zpomalovat) točivým elektrickým polem : podobně jako v iontových urychlovačích.
Ovšem nic není zadarmo ; vedle těchto podstatných výhod má tekutý Hyper-Rotátor také jednu velikou nevýhodu : supratekuté He vyžaduje nízkou teplotu cca -271°C (to však už nebude podstatnou překážkou) . Také koeficient strhávání bude zajisté menší, než u pevného HyRu.
Kapalinový HyR, tvořený supratekutým Heliem, pak bude proudit (vířit) v toroidální trubici , omotané příslušnými cívkami a elektrodami.
Alex Aleš Borek
| NAHORU na OBSAH | NOVÉ TEORIE a IDEJE |
|---|